对称加密与非对称加密
对称加密
对称加密使用同一个密钥完成加密和解密操作,通信双方都需要拥有此密钥。
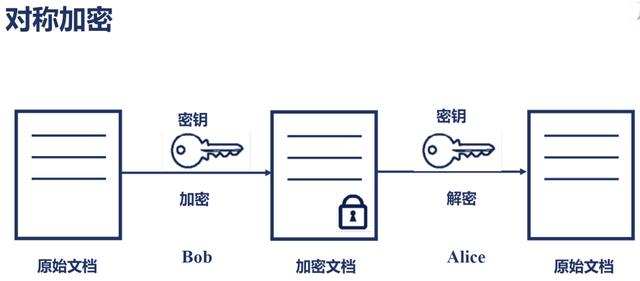
举个最简单的对称加密的例子,现有密钥 x,需要发送的信息为 m,加密的方法是用密钥做异或操作,加密后的内容为 m^x。对方收到信息后,在次使用 x 进行异或,即 m^x^x=m 这样就收到了原始信息了。这种方法太过简单不够安全。比如在通信中常常开始和结束的消息是固定的,由此窃听者就能猜测出传输的消息 m,进而破获密钥。即使这个例子不够安全,但是已经体现出了对称解密的本质。使用同一个密钥来完成加解密。
通常密钥的长度为几百字节,比如 256 字节,但是要发送的信息往往很长,加密过程是把原文分成和密钥等长的段来分别进行的。成熟的对称加密算法对数据做多轮加密,而且会做字节的移动等操作。解密时做逆操作即可。这样做的目的是为了防止绕开密钥破解出信息来。
对称加密的难点在如何让通信双方都拥有密钥。一种方法是提前在通信双方的机器上部署密钥,这只适用于固定的某些机器之前进行通信。另外一种方法是使用非对称加密技术来传输密钥。非对称加密,是下一节的内容。
非对称加密
非对称加密算法的代表位 RSA 算法,RSA 是三个发明人的首字母缩写。非对称加密中用于加密和解密的密钥是不同的。
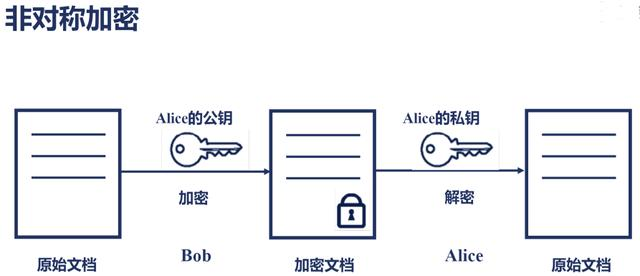
在非对称解密中,存在两个密钥——公钥和私钥,其中公钥是公开的,它可以通过明文传输。但是使用公钥加密后的加密文档必须使用私钥进行解密。私钥必须要保密,如果私钥被窃取了,非对称解密的安全性就不能保证的。
在 RSA 算法中,首先会挑选两个很大的素数 P 和 Q,两者相乘得到 N。取一个小于 (P-1)(Q-1) 且与之互质的数作为 e,公钥就由 (e, N) 两者组成。
N = P * Qe为某与(P-1)(Q-1)互质的数,通常选择较小的质数,这样加密速度比较快。
设需要加密的内容为 M,加密后的内容为 C,加密方法如下:
使用 e 和 P、Q 根据如下式子生成 d,私钥就由 (d, N) 组成。
有了密钥之后,可以用如下运算解密:
\[M = C^d \% N\]关于解密的运算,可以参见补充说明。
非对称加密的安全性
在非对称加密中,N 和 e 都是已知的,要想解密必须要知道 d,而要想计算出 d,必须知道 P 和 Q,但是目前对 N 进行质因数分解得到 P 和 Q 不存在有效的算法。因为 N 的长度通常达到几百位,想要暴力破解是不现实的,因此,非对称加密目前还很安全。
补充说明
其中 $e^{-1}$ 是 e 的倒数,对一个分数进行取模,这还是挺少见的,在此之前我是不知道如何做。关于取模有如下性质:
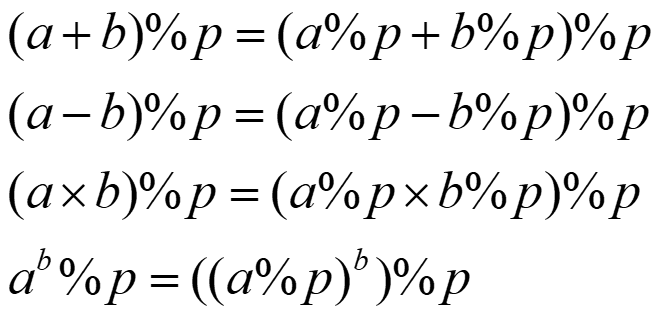
但是:
\[(a/b) \% p \ne (a\%p / b \% p) \% p\]所以加减乘、指数都好处理,但是除法不好办。在运算中如果中间结果很大,那么可以进行取余。但是一旦运算中出现了除法,就不好办了。此时需要使用逆元,将除法转换为乘法运算。
逆元的定义如下:

即如果 $(a*c) \% n = 1$ 那么 $(1/a) \% n$ 可以替换为 $c \% n$。
其实分数在平常使用的数学范畴里,确实是不能取余的,有悖于常识。上面的定义是来自数论中的理论。在数论中,除法的取余就是乘以除数的逆元。
对称解密和非对称解密的配合使用
非对称解密的运算量较大,通常在通信中常常使用非对称解密算法来传输用于对称加密的密钥,因为非对称加密可以安全地传输密钥,传输完密钥之后,可以切换至对称加密。在 HTTPs 中就是这么做的。