论文阅读 - Distributed Representations of Words - Mikolov 2013
今天讨论 Distributed Representations of Words and Phrases and their Compositionality。我认为这篇论文对 NLP 发展具有里程碑式的意义。这篇论文我很很久以前读,但是并没有完全搞明白。最近看论文牵扯到这里面的部分知识,发现自己似懂非懂,因此再次阅读这篇论文,并整理过去记录的关于此论文的笔记。
何为 Embedding
在传统的自然语言处理中,每个词被视为离散的符号,每个词用唯一的 id 来标识,词被表示为 one-hot 的向量,词与词之间没有任何关系。但实际上词之间具有明显的关系,比如“白色”和“黑色”都是表颜色的词,但是基于 one-hot 的表示法不能表示出词之间这种关系。
white = [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
black = [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
使用 one-hot 表示的词向量维度巨大(向量长度等于词表大小),且向量之间彼此正交(內积为0)。
后来人们想到可以把每个词用一个向量来表示,如果向量长度为 N,那么每个词都是 N 维空间中的一点。向量的每一个维度,可能表示词的某种特征。举个例子,比如某一维度可能表示这个词是否为表示颜色的词。当然各个维度代表的含义是隐含的,但用向量来表示词语,确实能够刻画词的不同特征。
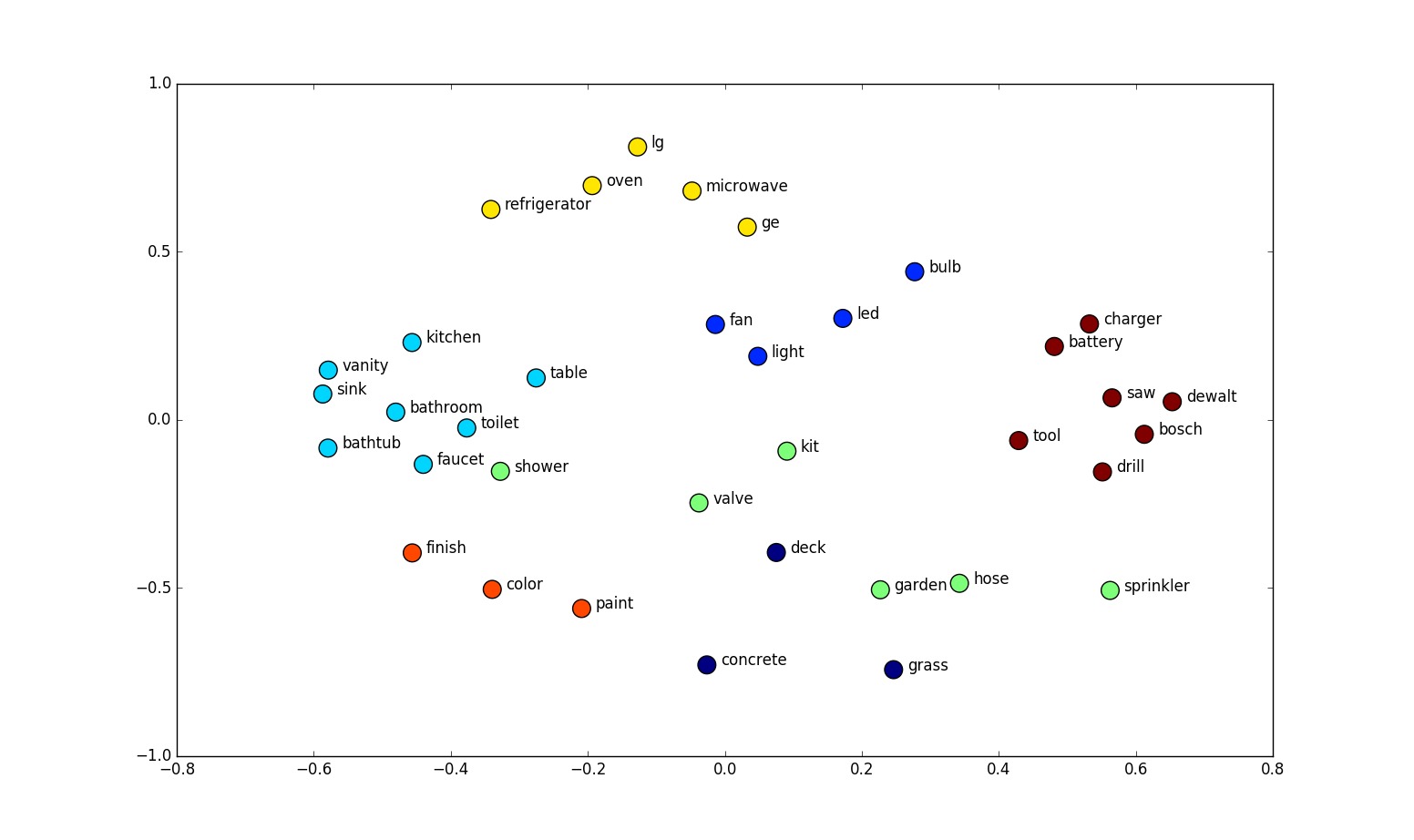
用来表示 word 的向量被称为 Embedding,因为这个词被嵌入到(embedded)了向量空间中。
如今 Embedding 已经是深度学习的标配了,最早 Embedding 用在 NLP 领域来表示一个词(word),后来在推荐系统中 Embedding 可以用来表示物品。词经过 Embedding 之后就变成了一个低维的稠密向量。

如何得到 Embedding
词的 Embedding 应该根据这个词的周围的其它词学习而来。
A word’s meaning is given by the words that frequently appear close-by.
words that occur in similar context tend to have similar meanings.
词向量都是利用大量的语料使用无监督学习得来的,其中最为知名的方法就是 word2vec 了。
Mikolov 等人在 2013 年左右,发布的一系列论文,提出了一种非常高效的模型,来训练词向量。
论文作者根据论文提出的原理,开发了一个程序 word2vec,以帮助人们用文本得出 Embedding,因为这个模型的巨大成功,word2vec 也就成了 Embedding 的代名词。后文将根据论文来讲讲具体原理。
word2vec
学习 Embedding 使用的是语言模型,传统的语言模型,是使用 n-gram 基于统计,来用前面的词预测后面的词。Mikolov 等人在论文 Efficient Estimation of Word Representations in Vector Space 中提出了两种新的语言模型:
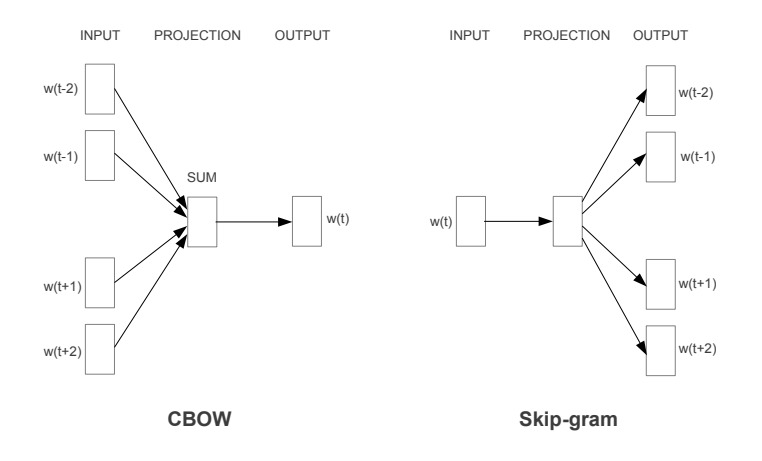
词在文本中是以序列的形式出现的,选择一个窗口,上图中窗口为 5。CBOW 是利用周围的词作为模型输入,预测中间的词。即以周围的词作为输入,采用一个分类模型,期待的输入是中间的词。Skip-gram 是使用中间词作为输入,期待模型输出为周围的词。
上面这个模型可以看做是一个两层的全连接神经网络,以 softmax 作为输出层。
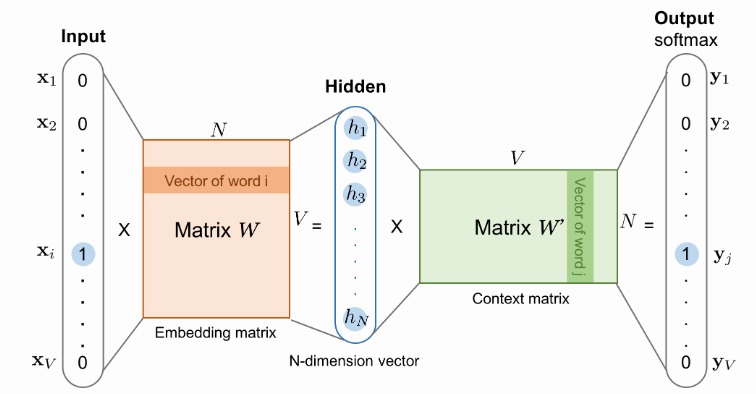
其中矩阵 $W$ 是第一个隐层的参数,$W’$ 是第二个隐层的参数。输入 $x$ 是 one-hot 表示的向量,输出是在各个词上的概率分布。
模型训练完成后,矩阵 $W$ 中第 $i$ 行,$W’$ 中第 $i$ 列,就可以作为词向量。这两个向量可以取其一,也可以相加或拼接。这正是 word2vec 的神奇之处,Embedding 居然是训练结束后的模型参数。
The Skip-gram Model
以 Skip-gram model 为例详述模型的训练过程。skip-gram model 是用中间的词预测周围的词。
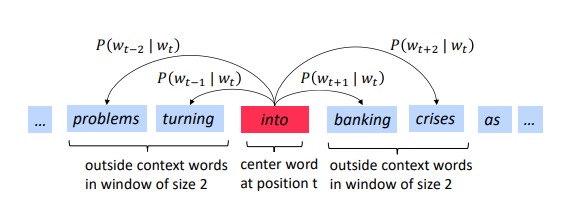
给定词序列 $w_{1}, w_{2}, w_{3}, \dots, w_{T}$,Skip-gram model 的目标函数是最大化下式:
\[\frac{1}{T} \sum_{t=1}^{T} \sum_{-c \leq j \leq c, j \neq 0} \log p\left(w_{t+j} | w_{t}\right)\]其中 $c$ 是窗口大小,$T$ 是词序列的长度。$\log p\left(w_{t+j} \vert w_{t}\right)$ 是以中间词为输入,输出周围词的概率。这个模型的目标就是最大化周围词的概率。
其中 $p\left(w_{t+j} \vert w_{t}\right)$ 该如何计算呢?
从前面模型的结构图可以知道,一个词对应两个向量,设:
- $v_{w_I}$ 表示词 w 在第一个矩阵中的向量
- $u_{w_O}$ 表示词 w 在第二个矩阵中的向量
如此以来,以词 $w_I$ 作为输入,词 $w_o$ 对应的概率为:
\[p(w_O \vert w_I) = \frac{\exp({v'_{w_O}}^{\top} v_{w_I})}{\sum_{i=1}^V \exp({v'_{w_i}}^{\top} v_{w_I})}\]有了目标函数,就可以使用梯度下降法来优化目标,更新模型参数了,但这个 softmax 需要很大的计算量,工程实现上不可行。
根据目标函数可以观察到,这个模型会希望中心词的输入向量和周围词的输出向量內积越大越好。就这样一个目标,为什么能够让出现在相同上下位的词具有相似的词向量呢?我想是这样的:对于“中国”和“美国”这两个词,它们的上下文是类似的。如果上下文中的词的向量固定不变,为了让內积最大化,“中国”和“美国”两个词的词向量需要做相同的调整。如果两个词的上下文完全相同,那么这两个词的词向量在训练过程中的调整过程完全一样,最终这两个词的词向量会完全相同。
Hierarchical Softmax
前面一节 softmax 的式子中,分母部分需要遍历所有词,而词的数量常常是几十万的量级,这一步就会非常耗时间。因此需要找的其他优化策略。
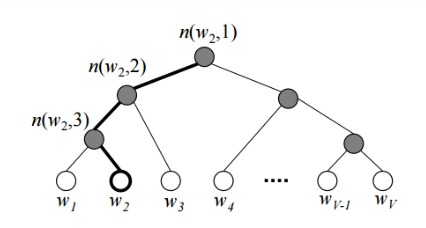
Hierarchical softmax 使用二叉树来记录所有的词,所有词被放在树的叶子节点(白色)上。每个内部节点(灰色)也有自己的词向量。基本想法是每个叶子节点的概率,都是从根节点到该叶子节点的路径上记录的概率之积。
当输入为 $w_I$ 期望输出(概率较大)之一 $w_O$ 而言,希望 $w_I$ 的向量与 $w_O$ 至根节点路径上的节点的向量內积越大越好。对于和 $w_O$ 出现在相同上下文的其他词,其词向量就需要做相应的调整以使其与路径上的节点之內积变大。
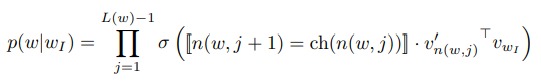
$L(w)$ 为树的深度,方括号里面是一个示性函数。从根节点到 $w_O$ 的路径上的所有节点,每次都随机选一个孩子节点,如果选则是路径上的节点,就返回 1,否则返回 -1。这么做就是希望处在路径上的节点的向量与 $w_I$ 內积越大越好,不再路径上的节点,內积越小越好。
这里选择孩子节点并不是选择上一次选择的节点的孩子。而是每次都取路径上的节点,然后选一个孩子节点。公式中 $n(w, i)$ 就是随机的节点。
这一部分还是挺难理解的,清楚真的有点困难,如果要深入理解,可以参考 Morin 和 Bengio 在 2005 年发表的论文。
Negative Sampling
Negative Sampling 也是为了缓解 softmax 计算量大的问题。其思想是,在训练过程中,取窗口中的 context word(周围的词)作为正例,在窗口外选取 $k$ 个词作为反例。
这样每次考虑到了词就很有限了,消除了 softmax 中求和的部分。对于窗口中心的词 $w_I$,窗口内周围的词 $w_O$ 以及随机抽取的词 $w_i$,期望下面式子取值最大:
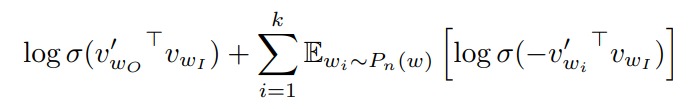
其中 $\sigma(x)=1 / 1+\exp (-x)$,$\mathbb{E}{w{i} \sim P_{n}(w)}$ 是指抽取的词 $w_i$ 服从某种分布(后文会讲到)。
上面式子直观理解就是,对窗口内的词期望向量內积越大越好,即 Logistics Regression 输出越大越好。对于随机在窗口外抽取的词,希望 LR 输出越小越好。
式中窗口外的词 $w_i$ 被抽到概率根据词频决定,被抽到的概率为:
\[P_{\alpha}(w_i) = \frac{c(w_i)^\alpha }{\sum_{j}^{T} c(w_j)^\alpha}\]其中 $c(w)$ 是词 w 出现的次数。$\alpha$ 是一个可调参数,用于对词频对高频词进行惩罚,对低频词进行补偿。
\[\frac{990}{990+10} = 0.99\] \[\frac{990^{0.75}}{990^{0.75}+10^{0.75}} = 0.97\]加入 $\alpha$ 参数后高频词被抽到的概率降低,低频词被抽到的概率会提高。
Subsampling of Frequent Words
一个词的 Embedding 是基于其上下文训练出来的,对于“法国的巴黎”这句话而言,上下文中“巴黎”对“法国”的影响很大,而“的”的影响几乎没有。另外高频词,如“的”,因为很很多词都在同一上下文共现,“的”的词向量更新并不会很剧烈,对 Embedding 的训练提供的帮助较小。
因此,在训练的时候,抛弃一些高频词,能够加快模型收敛速度,且让 Embedding 训练的更好。这里 Subsampling 的做法是在训练集中,将一部分词抛弃掉。
对词 $w_i$ 抛弃的概率用下面式子计算:
\[P\left(w_{i}\right)=1-\sqrt{\frac{t}{f\left(w_{i}\right)}}\]其中 $f(w_i)$ 表示词 $w_i$ 出现的频率。$t$ 是人为选定的一个值,一个参考值是 $10^{−5}$,选取的越小,抛弃的概率也就越小。
Embedding 的质量评价
人们发现使用 word2vec 得出的 Embedding 具有一些优良的性质。比如多个同种类似的词组在空间中具有平行关系。
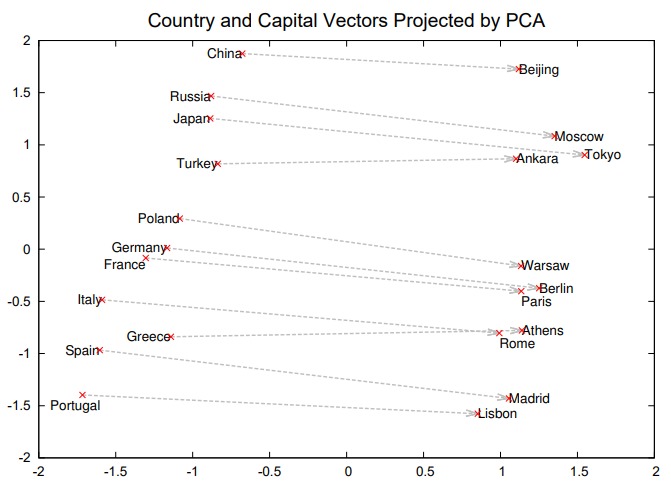
因而可以有下面性质:
vec(“Madrid”) - vec(“Spain”) + vec(“France”) = vec(“Paris”)
vec(“quick”) - vec(“quickly”) = vec(“slow”) - vec(“slowly”)
vec(w) 表示 w 的 Embedding,Embedding 的这种性质,让我们可以回答“西班牙之于马德里相当于法国之于 XXX ?”这样的问题。
因此有人构造了一组此类的数据,在这数据集上来计算 Embedding 的准确度。
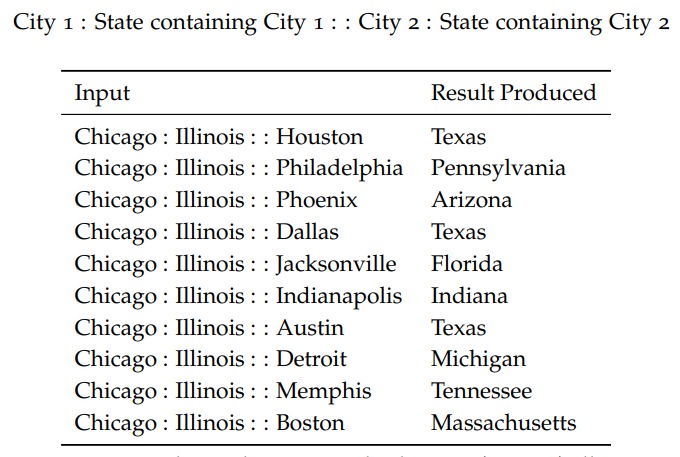
Embedding 通常作为其他任务的输入,比如问答或者完形填空:
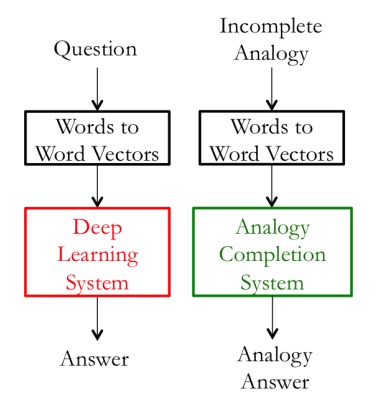
那么衡量 Embedding 好坏的另一种策略是直接衡量系统的效果,如果某个 Embedding 模型让整个 QA 系统效果提升,说明这个 Embedding 适合该场景,可以说它更好。
学习短语的 Embedding
短语由多个词组成,比如 “New York”,这个词的 Embedding 不能简单通过将 “New” 和 “York” 两个词的词向量加和得到。而需要在训练的时候就把它视为一个整体。
\[\operatorname{score}\left(w_{i}, w_{j}\right)=\frac{\operatorname{count}\left(w_{i} w_{j}\right)-\delta}{\operatorname{count}\left(w_{i}\right) \times \operatorname{count}\left(w_{j}\right)}\]论文中,作者基于共现统计找出了短语,将短语视为一个整体。
实验
实验显示增大窗口大小,能够提高 Embedding 的质量,使用更大规模的语料对提升 Embedding 质量有很大帮助。
CBOW 和 Skip-gram 两种模型训练出来的结果孰优孰劣,原论文中并没有谈到,但是很多其他论文有做过对比,后面要总结一下。
总结
第一次试图了解 word2vec 是半年前了,那个时候觉得这玩意很复杂,看了一遍论文之后,也没有理解清楚。后来在不同的地方见到别人讲,慢慢地清晰了不少。