训练深度网络
本文为阅读 Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow 的第 11 章时记录的笔记。
梯度消失 / 梯度爆炸
误差的梯度在反向传播的过程中,变得越来越小,最后近乎消失,这导致网络前面的层的参数得不到更新,无法收敛到最优解。
相反,梯度也可能变得越来越大,在反向传播的过程中,梯度越来越大,靠前的层的参数更新的非常剧烈,模型无法收敛。
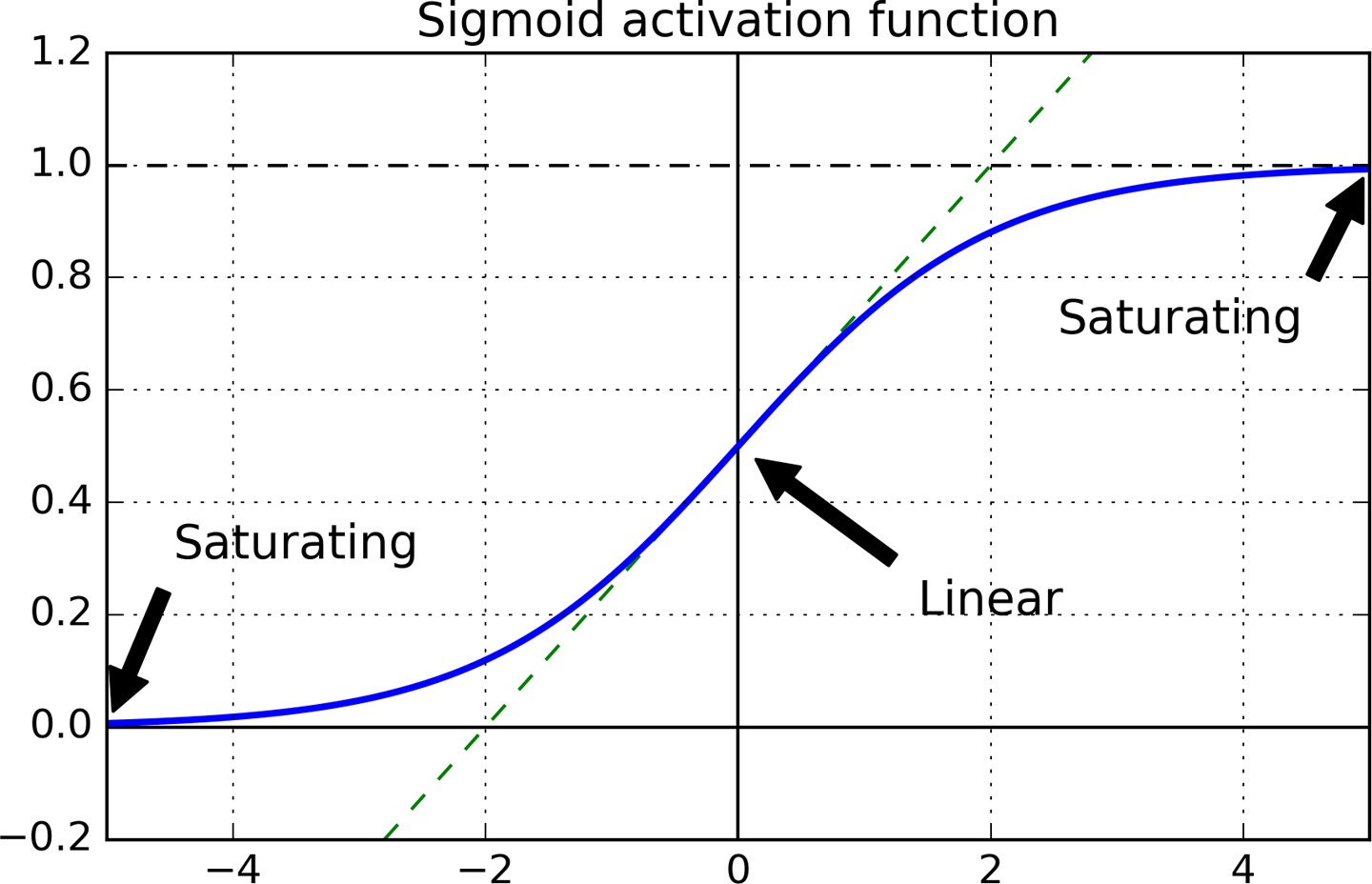
梯度消失的主要原因是使用 sigmoid 作为激活函数。从上图中可以看出,当输入很大或很小时 sigmoid 的函数曲线很平坦,其梯度都接近于 0,梯度最大时也才 0.25, 因此误差在反向传播时,经过激活函数后,梯度会很小。越先前传播梯度越小,导致网络中靠前的层几乎得不到更新。
另外由于 sigmoid 函数输出的均值为 0.5,这导致前向传播时,输入的方差越来越大。
参数初始化
Glorot 和 Bengio 早期的一篇论文 - Understanding the Difficulty of Training Deep Feedforward Neural Networks 指出,网络的输入和输出应该具有相同的方差。
在实践中,人们发现了针对不同激活函数的参数初始化策略。大体思路是将参数随机初始化为均值为 0 的高斯分布,方差的大小则根据激活函数来定。
下表做了总结:

fan_in 指输入的神经元数量,fan_out 为输出神经元数量,fan_avg 自然就输入输出的均值了。
激活函数
ReLUs
ReLUs 激活函数极大地缓解了梯度消失的问题,对于正输入值 ReLUs 不会饱和,且计算起来很快。
但依然存在问题,一旦某个 unit 输出小于 0,那么它之后就只会输出 0,而且梯度也会是 0,即 ReLU 也可能出现梯度消失的问题,此 unit 的权重将得不到更新。这个问题称为 Dead ReLUs。
Leaky ReLU

Leaky ReLU 可以让未激活 unit 在训练中有机会再次激活。
\[LeakyReLU_{\alpha}(z) = max(\alpha z, z)\]ELU
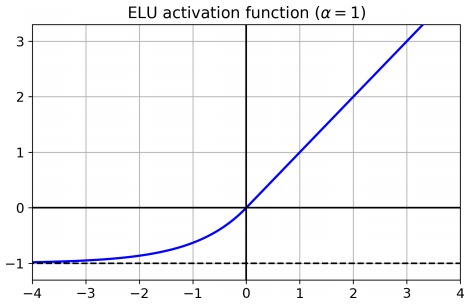
ELU 的特点是,其输出的均值接近为 0,同时再各个位置均可导。其数学定义如下:
\[\mathrm{ELU}_{\alpha}(z)=\left\{\begin{array}{ll}{\alpha(\exp (z)-1)} & {\text { if } z<0} \\ {z} & {\text { if } z \geq 0}\end{array}\right.\]Batch Normalization
使用 ReLU 及其变种,加上合适的参数初始化策略,在训练的初期可以很好地消除梯度消失/爆炸的问题,但不能保证在整个训练过程中都不出现梯度消失/爆炸的问题。Batch Normalization 对输入的整个 batch 的数据做标准化,可以持续减缓梯度消失/爆炸的问题。
Batch Normalization 需要调整的参数不多,momentum 用于计算动态调整的均值,它的值应该接近于 1。样本集越大,或者 batch-size 越小时,momentum 应该越接近于 1。在训练过程中需要在用每个 batch 的均值和方差来调整整体的均值和方差,momentum 是用来做平滑的。
如果在输入层之后紧接一个 batch normalization 层,对数据做标准化操作就可以不用显式地完成了。
梯度裁剪
梯度裁剪是限制梯度的大小不超过某个阈值。在 RNN 中梯度裁剪尤其重要,因为 RNN 常常出现梯度爆炸的问题。
optimizer = keras.optimizers.SGD(clipvalue=1.0)
model.compile(loss="mse", optimizer=optimizer)
在 keras 中设置梯度裁剪尤其简单,以上代码将限制梯度的绝对值小于 1.0。对梯度的某个分量进行裁剪,会导致梯度方向的改变,比如原梯度为 [100, 1], 裁剪后变为 [1, 1],这极大地改变了梯度方向。要想保证梯度方向不变,可以对梯度的 L2 范数做限制,即限制梯度向量的模长。下面的设置保证梯度的模长不大于 1,否则各个分量都进行缩减,保证梯度方向不变。
optimizer = keras.optimizers.SGD(clipnorm=1.0)
优化器
Momentum
模拟石头滚下山的状态。在平坦的函数平面上因为有惯性的存在,能够快速通过平坦区域。

optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)
Nesterov Accelerated Gradient

在计算新的梯度时,考虑到已经加入的动量。下图中左边的蓝色短线表示当前的梯度方向,黑色长线是动量,两者之和应该是蓝色的虚线。NAG 的策略是不在当前点计算梯度,而是想用动量走一步,然后在新走的哪一点计算梯度。即在黑线箭头位置计算梯度。
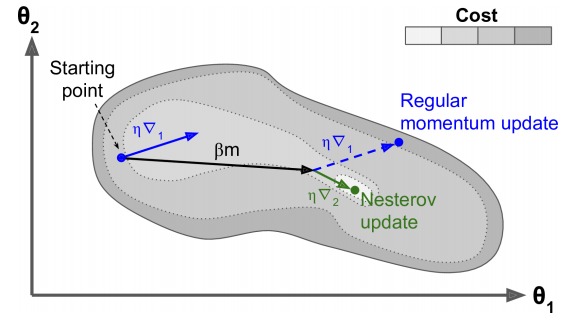
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)
AdaGrad
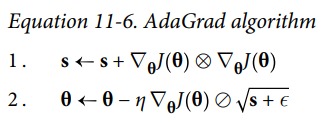
梯度小的方向,大幅更新。梯度大的方向,小幅度更新。
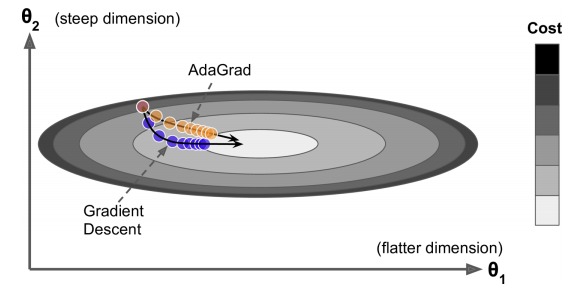
上图中,水平方向较长,较平坦,梯度较小。竖直方向,梯度较大。常规的梯度下降法,会走蓝色路径。而 AdaGrad 会走橙黄色路径。
但是 AdaGrad 不断地对梯度值进行累加,最终导致上面式子中 s 的值过大,更新越来越慢,可能还没有到最优点时,就更新不动了。
RMSProp
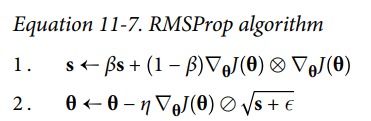
RMSProp 修复了 AdaGrad 的问题,通过引入一个衰退系数,让 s 仅仅累加最近的梯度。
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)
Adam and Nadam

Adam 综合了 RMSProp 和 Momentum。3 4 两个式子中 t 代表的是迭代次数,当迭代次数较小的时候,m 和 s 的值能够被放大,当迭代次数增大是分母也就很接近 1 了,m 和 s 的值就不会在被放大了。这是为了在迭代的初始时,m 和 s 的值为 0,通过这两个式子,可以对初试阶段进行加速。
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
Nadam 是在 Adam 中加入了 Nesterov Accelerated Gradient 中的思想。
学习率调整策略
如果学习速率过大,模型会发散,学习速率过小,模型收敛太慢。学习速率稍微大了点,那么最终会在最优解附近震荡。
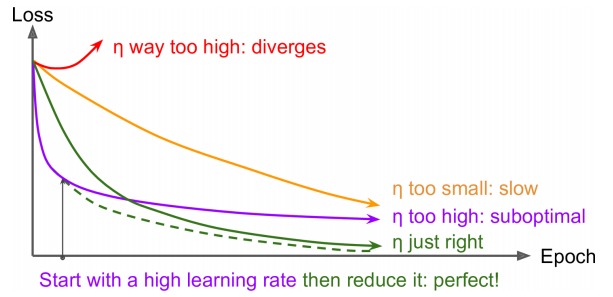
训练的不同阶段,最佳学习率往往不一样,在学习过程中动态的调整学习率,是一个很直觉的想法。常用的学习率挑战策略有下面一些:
Power scheduling
学习率与 step 数成反比,随着参数更新次数的增加,学习速率慢慢降低。具体的更新公式如下:
\[\eta(t)=\eta_{0} /(1+t / k)^{c}\]其中 c 通常为 1,k 为常数,t 是 step 数。可以看到 k steps 之后,学习率减半,2k steps 之后,学习率减小为 1/3。
在 keras 中实现 power scheduling 很容易。
optimizer = keras.optimizers.SGD(lr=0.01, decay=1e-4)
decay 是前面式子中,k 的倒数。
Exponential scheduling
没过 $s$ steps 学习率减少 10 倍。
\[\eta(t)=\eta_{0} 0.1^{t / s}\]在 Keras 中实现的方法如下:
def exponential_decay_fn(epoch):
return 0.01 * 0.1**(epoch / 20)
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, [...], callbacks=[lr_scheduler])
Piecewise constant scheduling
训练的不同阶段使用不同的学习率,实际上就是一个分段函数:
def piecewise_constant_fn(epoch):
if epoch < 5:
return 0.01
elif epoch < 15:
return 0.005
else:
return 0.001
Performance scheduling
当验证集上的 loss 不再下降的时候减小学习率。比如 5 个 epoch loss 不降,就把学习率减小一半:
lr_scheduler = keras.callbacks.ReduceLROnPlateau(factor=0.5, patience=5)
正则化
L1 L2 正则化
就像训练线性回归模型时那样,也可以给神经网络加入 L1 或 L2 正则化项。
from keras import regularizers
keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=regularizers.l2(0.01))
# L1 regularization
regularizers.l1(0.001)
# L1 and L2 regularization at the same time
regularizers.l1_l2(l1=0.001, l2=0.001)
Max-Norm Regularization
一个神经元,其数学表示为 $\sigma(w x + b)$,max-norm regularization 并不在损失函数中增加正则化项。它限制 $w$ 的模长,如果 $w$ 中的某一维度的值过大,那么其模长会变大,限制模长能够从一定程度上限制参数的大小。通常在训练的每一步之后,如果 $w$ 大于阈值,就对其做调整,调整策略如下:
\[w \leftarrow w \frac{r}{\Vert w \Vert _2}\]在 keras 中,可以采用如下代码实现。
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal",
kernel_constraint=keras.constraints.max_norm(1.))
Dropout
原理
在训练过程中随机将输出中的一部分置 0,这让神经元间的彼此依赖减弱。一个类比是,在一个大公司里,每天都随机有一部分员工不来上班,因此每个员工就不得不和更多的同事建立合作,这样公司才能运转下去。
因为有 dropout 的存在,训练阶段,每个 step 都是网络中部分神经元在协作。在测试阶段,所有神经元都一起工作,有种将很多网络集成起来的感觉。
在测试阶段,因为没有 dropout 存在,输出的所有维度都有值,激活函数的输入看起来会大一倍,因此在测试阶段给输出再乘一个 dropout rate,将各个维度的值减小。
还有一种做法,在训练阶段,对输出作了 dropout 之后,将值全部扩大一倍。这样以来,在测试阶段,就不再对输出作任何操作了。
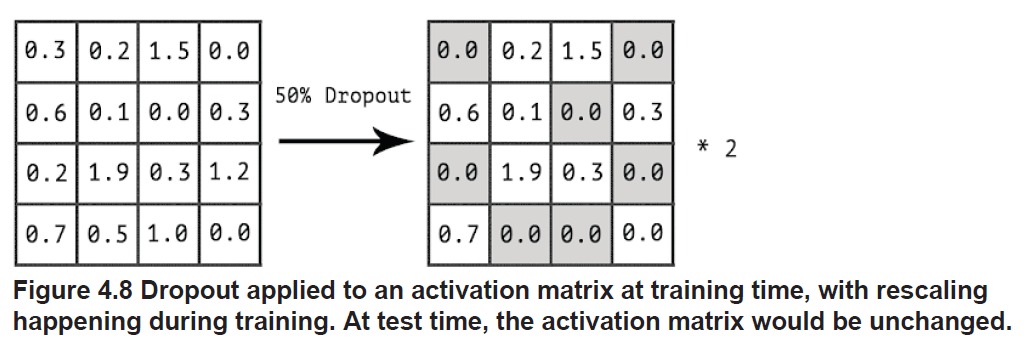
但是这一切在 Keras 中都可以交给 Dropout 来处理。
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])
Monte-Carlo (MC) Dropout
如果把 Dropout 看做是神经网络的集成,那么在预测的时候,应该是多个模型进行投票。Monte-Carlo Dropout 策略就是在预测阶段,开启 Dropout,然后预测 n 次,n 次的结果进行投票,或者对概率求均值。
with keras.backend.learning_phase_scope(1): # 强制开启 dropout
y_probas = np.stack([model.predict(X_test_scaled)
for sample in range(100)])
y_proba = y_probas.mean(axis=0)
采用开启 Dropout 得出的多个结果综合得出预测结果,看起来比关闭 Dropout 后得到单次预测要靠谱。
对一个样本关闭 Dropout 后得出的预测概率如下,看起来对最后一类很确信。
[[0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.99]]
而关闭 Dropout 后,进行多次预测,可以看出模型有时候对最后一类并非很确信。
[[[0. , 0. , 0. , 0. , 0. , 0.14, 0. , 0.17, 0. , 0.68]],
[[0. , 0. , 0. , 0. , 0. , 0.16, 0. , 0.2 , 0. , 0.64]],
[[0. , 0. , 0. , 0. , 0. , 0.02, 0. , 0.01, 0. , 0.97]]]
最终求均值后得出的结果如下:
[[0. , 0. , 0. , 0. , 0. , 0.22, 0. , 0.16, 0. , 0.62]]