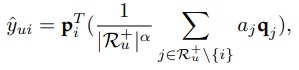Item Similarity Model
- Item-based CF
- 矩阵分解
- SLIM (Sparse LInear Method)
- FISM (Factored Item Similarity Model)
- NAIS (Neural Attentive Item Similarity)
Item-based CF
基于 user-item 评分矩阵,利用 cosine 或者 Pearson correlation 来计算 item 间的相似度。user $u$ 对 item $i$ 的评分估计值为:
\[\hat{y}_{u i}=\sum_{j \in \mathcal{R}_{u}} r_{u j} s_{i j}\]其中 $\mathcal{R}_{u}$ 是 user $u$ 所有评分过的 item 集合,$s_{i j}$ 是 item $i$ 和 item $j$ 的做了标准化后的相似度。
这种方法直接、易行,但是在相似度的度量上,由于矩阵的稀疏性,相似度计算效果不是特别好,推荐质量不够高。
矩阵分解
矩阵分解的策略是将 user-item 评分矩阵分解为两个低秩的稠密矩阵:
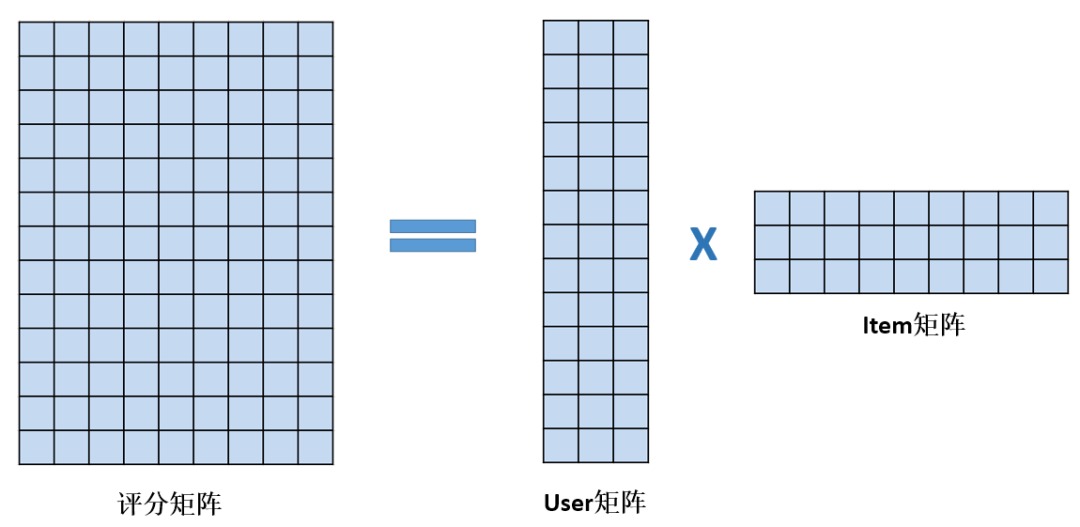
在推荐时,可以使用 user 的向量乘上 item 矩阵,得到该 user 对所有 item 的评分的估计值,然后得出推荐结果。
但是当 user 与新的 item 产生交互时,user 和 item 的向量应该发生变化。尤其是对 user 而言,要想具有实时性,user 最近的交互信息就一定要能够影响 user 的向量。但是矩阵分解的方法没法做到这种实时性。
利用分解得到的 item 矩阵,也可以计算 item 之间的相似度,而且比直接用 user-item 评分矩阵来计算相似度效果更好。因此矩阵分解也可以用在传统的 item-based CF 中,用于计算 item 间的相似度。
SLIM (Sparse LInear Method)
论文 SLIM: Sparse Linear Methods for Top-N Recommender Systems 中提出一种方法直接学习出 item-item 间的相似度矩阵。
在约束条件下,最小化下式中的 $L$ :
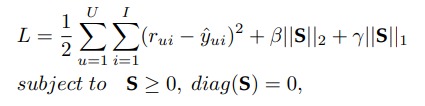
其中 $S \in \mathbb{R}^{I \times I}$ 是 item 间的相似度矩阵,加入 L2 正则是为了避免过拟合,加入 L1 正则化是希望相似度矩阵尽可能地稀疏,因为相似的 item 不应该很多。$S \ge 0$ 是因为相似度应该介于 0~1 之间。$diag(\mathbf{S})$ 则是要求 item 和自己的相似度为 0。
利用 user-item 评分矩阵中已有的评分数据来上上式最小化,可以学习得到一个相似度矩阵 $S$。
SLIM 模型的缺点很明显,矩阵 $S$ 的规模很大,训练起来很慢。另外只有 item $i$ 和 item j 同被一个 user 评分过,$S_{ij}$ 才能得到学习。
FISM (Factored Item Similarity Model)
出自论文 FISM: Factored Item Similarity Models for Top-N Recommender Systems。
如果将 item-item 相似度矩阵分解为两个低秩矩阵相乘,即 $S = PQ$。那么 item $i$ 和 item $j$ 之间的相似度表示为 $sim(i,j)=p_i · q_j^T$。
如此以来 user $u$ 对 item $i$ 的评分可以表示为:
\[\hat{r}_{u i}=b_{u}+b_{i}+\sum_{j \in \mathcal{R}_{u}} \mathbf{p}_{j} \mathbf{q}_{i}^{T}\]$b_u$ 和 $b_i$ 为 user 和 item 的 bias,其中 $\mathcal{R}_{u}$ 是 user $u$ 所有评分过的 item 集合,这里采用的可能是隐式反馈,集合中的 item 的评分都是 1,这是为啥没有评分值 $r_{ui}$ 的原因。
优化目标为:
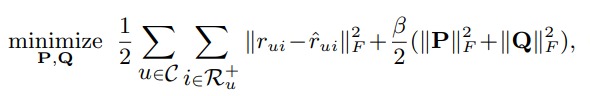
NAIS (Neural Attentive Item Similarity)
论文 NAIS: Neural Attentive Item Similarity Model for Recommendation 在 FISM 的基础做了改进,加入了 Attention 机制。
这里作者将 $p$, $q$ 都视为 item 的 Embedding,作者认为用户评分过的 item 的 Embedding 的均值可以作为 user 的 Embedding。这样以来评分 $\hat{y}_{u i}$ 的计算就很直接了,user embedding 乘上 item embedding 即可。
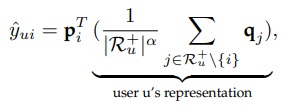
想象一下,如果 item 是一个衣服,那么在表示用户时,用户购买的衣服的信息就更重要一些。所以这里给用户评分过的 item 加一个权重,加权得到用户的 embedding。
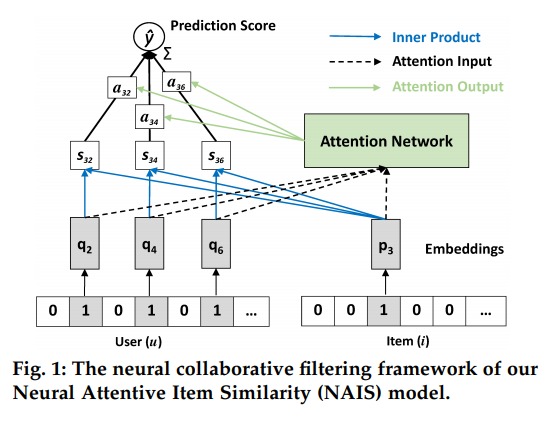
加入 Attention 之后对评分值得估计就变成了这样: