多种多样的卷积
多输入通道
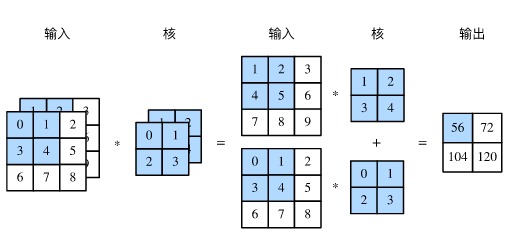
此图引用自 动手学习深度学习
对一个二维张量做卷积操作,很容易理解。当输入是多通道时,比如 RGB 三通道的图片,卷积核作用在三个通道上就会产生三个输出。如果有 10 个卷积核,岂不是有 30 个输出了。这是我最初的想法,后来发现事实并非如此。对于三通道的输入,5*5 的卷积核,其实会含有 5*5*3=75 个参数,也就是说卷积核也是三个通道,三通道的卷积核在三通道的输入上上下左右移动着做 element-wise 的相乘并求和,最终的结果就是一个一通道的输出。最后再在这个输出上加一个 bias。这就是多输入通道时,卷积核工作方式。
所以其实这里的卷积核仔细想来,应该是三维的。这样的卷积才能够捕捉到不同通道之间的关系。
多输出通道
如果输入是 3 通道,卷积核大小为 5*5,输出是 10 通道,这种情况该怎么办?根据前面对多输入通道卷积工作过程的描述,就不难理解,输出为 10 通道,上例中只要有 10 个核就可以了。
1D 卷积
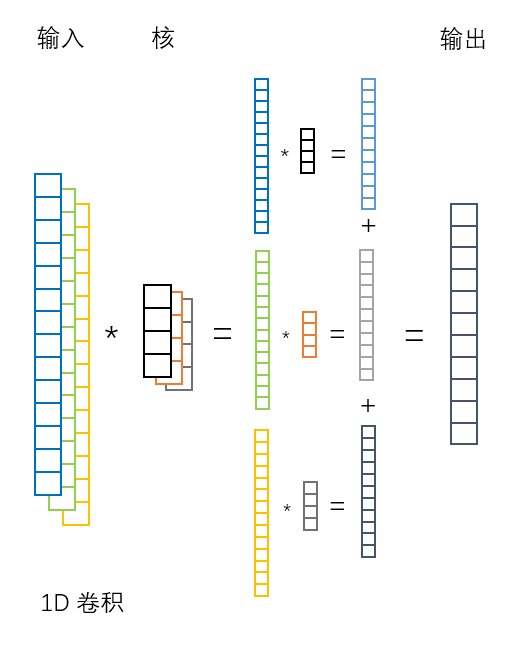
1D 卷积,输入数据是一维的,他可以有多个通道,但每个通道都是一维的。因此一维卷积的卷积核也是一维的,它在输入数据上做一维的移动,并做卷积。最终多个通道相加,得到一个一维的输出。
1x1 卷积
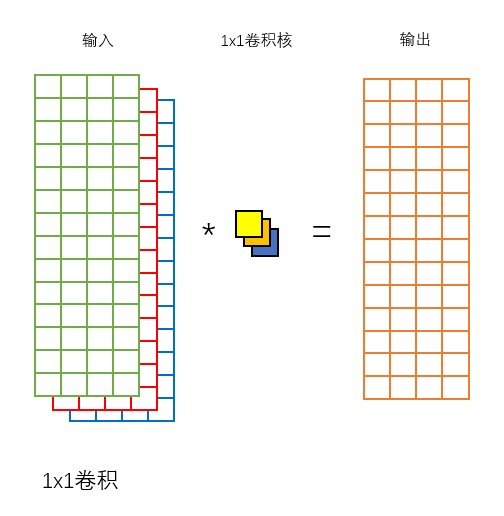
1x1 卷积可以看做是对输入的不同通道做了线性加权求和。
可分离卷积
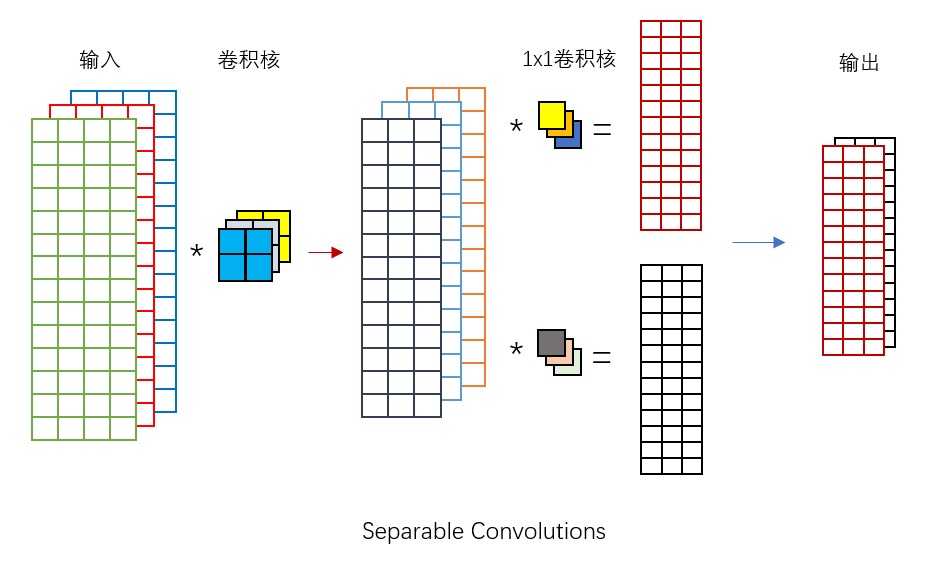
在 keras 中看到 SeparableConv2D 这个类,直译过来就叫做可分离卷积,所以暂且就这么称呼它了。
对常规的 Conv2D 而言,假设输入为 3 通道,卷积核为 5*5,输出为 10 通道,那么一共需要 3*5*5*10+10=760 个参数,但是对于 SeparableConv2D 而言,只需要 3*5*5 + 10*3 + 10 = 115 个参数。
如上图所示,可分离卷积对输入的 3 个通道做了 layer-wise 的卷积,即一个卷积核对一个输入层对应着来做卷积,得到 3 个输出层。然后并不做加和,这是和通常的卷积核区别,这里使用 2 个 1x1 的卷积来对这 3 个中间的输出层做线性组合,最终得到 2 个输出层。可分离卷积输出的通道数是由 1x1 卷积核的个数来决定的。