论文阅读 - Collaborative Filtering Survey
本文是我大约一年前在读论文 A Survey of Collaborative Filtering Techniques 时记下的笔记,但是写的比较凌乱。现在重新整理了,并结合自己的理解做了一些补充。有些章节感觉读综述搞不明白,需要深入读相关论文才行,这些部分没有记录。
1. 介绍
如今人们越来越依赖于推荐系统,推荐系统帮助人们筛选书籍、电影、音乐等内容。协同过滤(Collaborative Filtering, CF)作为一种推荐技术,被广泛运用于各种物品的推荐中。它利用群体的智慧,基于用户的行为来生成推荐,而不关注推荐的内容是什么。CF 的基本假设是:如果用户 X 和用户 Y 对 n 个物品有相似的评价(喜欢或不喜欢、评高分或评底分),那么在未来他们对另一个物品可能依然有相似的评价。
早期的 CF 系统,使用用户评分来计算用户或者物品之间的相似度,并依此来产生推荐。这些评分数据要放在内存中,便于计算相似度并生成推荐,因此被称为 memory-based CF。但是因为 memory-based CF 方法中计算相似度依赖于用户对物品的评分,因此容易因为评分数据量少,而无法准确地找到相似的用户或物品。
为了克服上面提到的问题,得出更好的推荐,人们提出了 model-based CF 方法。Model-based CF 是利用用户的评分数据学习出一个模型,并用此模型产生推荐。这个模型可以是一个数据挖掘或者机器学习的方法。常见的方法有:贝叶斯置信网络模型、聚类模型、隐式语义模型,还有马尔科夫决策过程。
除了协同过滤,基于内容的过滤是推荐系统中另一类重要方法。基于内容的推荐系统通过分析文本内容来找出文本中的规律,并据此生成推荐。基于内容的推荐系统依靠用户或物品的描述信息或特征,而不依赖用户的行为。而 CF 仅仅依赖用户的行为数据。
协同过滤推荐系统和基于内容的推荐系统都各有缺点,因此人们也常常混合使用二者,这样的系统被称为混合推荐系统。混合推荐系统综合两者,试图让两种方法互为补充。
2. 协同过滤的特点和挑战
数据稀疏
许多商业推荐系统,因为用户和物品的数量都很庞大,这导致 user-item 矩阵非常稀疏,因为缺少足够的数据,导致难以找到相似的用户或物品。
当新用户加入系统时,由于该用户尚未消费记录,无法给他任何有效的推荐。当新物品加入系统时,因为尚未有人消费过它,它也因此不会被推荐给任何人。这类问题,被称为冷启动问题。
覆盖率指推荐系统可能会推荐的物品在整个物品中的占比。数据稀疏还会导致能够得到推荐的物品的比例(即覆盖率)很低。因为那些物品还没有用户交互信息,因此推荐算法在计算时不会把它们作为结果。
为了解决数据稀疏性问题,人们提出了不少方法。降维技术,如奇异值分解(Singular Value Decomposition, SVD),移除了不具代表性和不重要的用户和物品来降低 user-item 矩阵大小。信息检索中用到的隐含语义指数(Latent Semantic Indexing, LSI)就用到了 SVD。相似的用户,通过降维后的矩阵来寻找。但是当某些用户和物品的信息经过降维后消失了,这样针对他们的推荐效果也会变差。
可扩展性
随着用户和物品的数据急剧增加,传统的 CF 方法面对巨大的性能问题,消耗的计算资源在实践上变得难以接受。在还有几百万乃至千万用户的系统中,即使是 O(n) 的复杂度都已经很大了。而且一些系统还要做到实时地根据用户最新行为作出响应。
降维技术能够具有很好地可扩展性,但是需要大量的离线预处理步骤。如 item-based 的方法具有不错的扩展性。在计算物品相似度的时候,并不计算所有物品之间的相似度,而是计算有共同点击的物品之间的相似度,这就大大降低了物品相似度计算这一步骤需要的计算量。
Modal-based CF 算法,比如聚类 CF 算法,对用户聚类,然后在小的范围内来寻找相似用户,通过这样的方式提高可扩展性。但这种方法会导致找到的相似 user 或 item 不是最优的,会降低推荐效果。这需要在可扩展性和模型精度之间进行权衡。
作弊问题
人们可能大量地给自己的物品刷好的评价,而给竞争对手的物品大量差评,这样推荐系统可能会倾向于推荐这些得到很多好评的物品。
其他问题
隐私问题:协同过滤推荐系统可能将别人消费过的物品推荐给另一人,这样就无形中透露了别人购买过什么东西,有的场景下,可能出现隐私泄露问题。
可解释性:让用户知道推荐此物品的原因,对用户可能会有用
3. Memory-Based CF 技术
Memory-Based CF 依赖于整个 user-item 矩阵,其中 neighborhood-based CF 是一种很流行的 memory-based CF 方法。它计算两个 user 或者两个 item 之间的相似度,找出与 user 或者 item 最相似的一组 user 或 item,称之为近邻。得出近邻之后,利用这近邻生成推荐结果。
3.1 相似度计算
相似度计算是 memory-based CF 推荐系统中的关键步骤。对于 Item-based CF,基本的思想是计算那些被一用户同时评分过的 item 们,并计算这些 item 的相似度。即在论文 Amazon.com Recommendations: Item-to-Item Collaborative Filtering 中给出的下图中的算法。

对于 user-based CF,计算对某个物品同时进行过评分的两个用户之间的相似度。这样做的好处是避免进行大量不必要的计算,因为没有被某个用户同时评分的两个 item 之间的相似度是 0。没有同时购买过同一个 item 的两个 user 之间的相似度也是 0。
下面列举相似度计算的几种方法:
3.1.1 Pearson correlation
Pearson correlation,皮尔森相关系数,用来反映两个变量线性相关程度。在 user-based CF 场景下,就是用来来计算两个用户 u 和 v 之间相似度:
\[w_{u, v}=\frac{\sum_{i \in I}\left(r_{u, i}-\overline{r}_{u}\right)\left(r_{v, i}-\overline{r}_{v}\right)}{\sqrt{\sum_{i \in I}\left(r_{u, i}-\overline{r}_{u}\right)^{2}} \sqrt{\sum_{i \in I}\left(r_{v, i}-\overline{r}_{v}\right)^{2}}}\]其中 $I$ 是 user u 和 user v 共同评分过的 item 的集合。$\overline{r}_{u}$ 是 user u 的平均评分。$r_{u, i}$ 是 user u 对 item i 的评分。
这里减去评分平均值,是考虑到不同用户评分时候的严格程度是不同的。如下图:
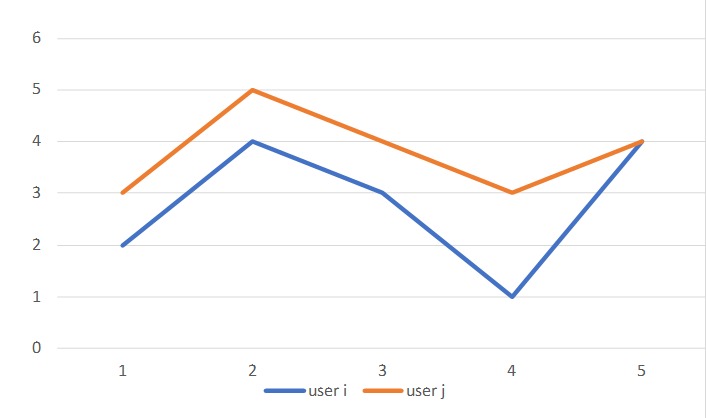
两个用户虽然给不同的电影评分都不同,但他们对同一部电影的看法是相似的,这可以说明这两个 user 具有相似品味。
3.1.2 基于向量的余弦相似度(Vector Cosine-Based Similarity)
要计算两个文档的相似度,可以用一个表示词频的向量来表示文档,而后计算两个向量的夹角的余弦值。夹角越小说明两个向量越相近,两个向量越相近,这个余弦值就越接近 1。这个方法可以用于协同过滤中计算 user-user 或 item-item 相似度。
要计算 user-user 相似度,就采用两个 user 对所有 item 的评分向量,采用如下计算公式:
\[w_{i, j}=\cos (\vec{i}, \vec{j})=\frac{\vec{i} \bullet \vec{j}}{\|\vec{i}\| *\|\vec{j}\|}\]同样的,计算 item-item 相似度,就采用这两个个 item 受所有 user 的评分的向量,同样采用上式。
3.1.3 改进的余弦相似度
使用基本的余弦相似度存在一个缺点,没有将用户的打分尺度考虑进去,即,有的用户的打分范围在 1~5 之间,而有的用户在 2~4 之间。这导致的后果是,习惯于给低分的用户的作用被削弱了。
比如,两个 item 有两个 user 给评分,分别是 item1 defen (10, 2),item 2 得分(10, 3),从下图中可以看出,在计算两个向量的夹角的时候,由于一个方向的值较大,两个向量的夹角很小,即相似度会很高。
但是 user 1 可能习惯于打高分,他认为最差的 item 也能得到 6 分,而 user 2 较严格,他打得最高分也就 4 分,即 4 分在他看来已经是很棒的电影了。为了让要求严格、打分低的用户的数据也能起到作用,而不是被其他习惯于打高分的用户的数据盖掉,从评分中减掉平均值。
可以看到,右图中,减去平均值后,角度差异变大了,即不那么相似了。
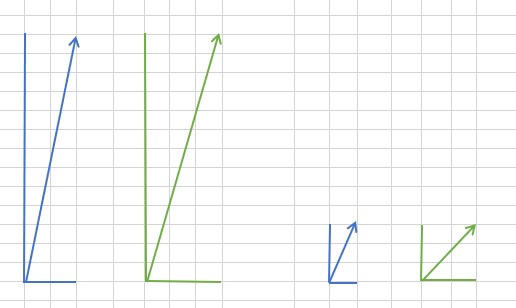
计算 item I 和 item j 的相似度,同样是使用对这两个 item 共同评分过的 user 的评分信息:
\[\operatorname{sim}(i, j)=\frac{\sum_{u \in U}\left(R_{u, i}-\overline{R}_{u}\right)\left(R_{u, j}-\overline{R}_{u}\right)}{\sqrt{\sum_{u \in U}\left(R_{u, i}-\overline{R}_{u}\right)^{2}} \sqrt{\sum_{u \in U}\left(R_{u, j}-\overline{R}_{u}\right)^{2}}}\]3.2 预测结果和推荐结果的计算
最终对 user-item 矩阵中缺失值的预测以及得出推荐结果是协同过滤中最重要的一步。在 neighborhood-based CF 算法中,与待推荐对象( active user ) 最相似的一组 user 被找出来作为 active user 的近邻。而后对这组近邻的产生的评分进行加权求和,得出对 active user 还为评分过的 item 的预测评分,利用这些预测的评分结果,挑出高评分的 item,生成推荐。
3.2.1 加权和
对于 user-based CF 算法,user a 对 item I 的预测评分值,可以参与加权和计算:
\[P_{a, i}=\overline{r}_{a}+\frac{\sum_{u \in U}\left(r_{u, i}-\overline{r}_{u}\right) \cdot w_{a, u}}{\sum_{u \in U}\left|w_{a, u}\right|}\]W 为 user a 和 user u 的相似度,即使用相似度作为权重。这里 U 则是 user a 的近邻的集合。
3.2.2 简单加权平均值
对于 item-based CF,用户 u 对 item I 的评分可以采用如下公式计算:
\[P_{u, i}=\frac{\sum_{n \in N} r_{u, n} w_{i, n}}{\sum_{n \in N}\left|w_{i, n}\right|}\]即用该用户已经评分过的 item 的评分值,来预测对未评分的 item i 的评分。这里 w 是 item i 和其他 item 之间的相似度。
3.3 Top-N 推荐
User-Based Top-N
User-based Collaborative filtering 基于一个假设,有相似偏好的用户在短期内依然会有相似偏好。设想一个电商平台场景,和某个用户相似的其他用户购买过的物品,该用户很可能也想要购买。因为他们存在相似性。
为了便于描述,将待推荐物品的用户称为 active user,将相似用户称为 sim users。User-Based CF 寻找和 active user 相似的其他用户(sim users)。收集 sim users 购买过的物品,对这些物品排序取 top N 推荐给 active user。
用户对物品购买与否可以构成一个 user-item 矩阵:
| - | item 1 | item 2 | item 3 | item m |
|---|---|---|---|---|
| user 1 | 1 | 0 | 1 | 1 |
| user 2 | 1 | 1 | 0 | 1 |
| user 3 | 0 | 1 | 1 | 0 |
| user 4 | 1 | 1 | 1 | 1 |
矩阵中 1 表示对应用户购买过对应物品,0 表示还没有购买过。在 user-item 矩阵中每个用户都对应一个向量,用户的相似度可以使用此向量夹角的余弦值来衡量,基于此相似度找到 k 个相似用户。令 sim users 购买过,而 active user 没购买过的物品集合为 $U$,这个集合中的物品就是潜在的 active user 会购买的物品。如何从中得出 N 个物品做为推荐结果呢?
统计集合 $U$ 中的物品出现的频次,这个频次是指物品被这些相似用户喜欢的次数。用频次作为排序依据,得出 Top N。考虑到非常热门的物品,会被很多人购买,其频次自然很高,但是老是推荐热门的物品缺少个性化,因此可以使用物品总购买次数除以前面提到的频次,以此来降低高频物品的权重。
考虑到用户相似程度不同,计算频次的时候可以考虑使用加入用户相似度。大体思路如下:
def recommend(active_user, n=20):
item_weight = defaultdict(float)
sim_users = find_sim_users(active_users)
for user, sim in sim_users:
for item in user.purchased_items:
item_weight[item] += sim # <-- 考虑到用户相似度
items = list(item_weight.keys())
items.sort(key=lambda item: item_weight[item], reverse=True)
return item[:n]
User-Based Top-N 推荐算法,可扩展性不佳,实时性不够好。因为用户行为多变,寻找近邻的过程需要在线实时计算。如果离线计算好,那么当用户新购买、收藏了某些东西后,不能依照这部分新产生的数据得出最新匹配的近邻。
Item-Based Top-N
Item-Based CF 算法基于大假设是,和用户喜欢过的物品类似的其他物品,该用户也可能会喜欢。因为物品的属性常常变化较小,物品之间的相似度变化的会较缓慢,因此 item-based CF 可以离线计算物品相似度,可以保证在线上有较好的性能。
- 为 active user 购买过的 item ,各自找 k 个相似的 item,构成集合 C;
- C 中的 item 与 active user 购买过的 item,计算加权和,找出 Top N。
大体思路如下:
def recommend(active_user, n=20):
purchased_items = active_user.purchased_items
all_sim_items = set()
for item in purchased_items:
sim_items = find_sim_items(item)
all_sim_items.update(sim_items)
item_weight = {}
for sim_item in all_sim_items:
sum_sim = sum(compute_sim(sim_item, item) for item in purchased_items)
sim = sum_sim / len(purchased_items)
item_weight[sim_item] = sim
items = list(item_weight.keys())
items.sort(key=lambda item: item_weight[item], reverse=True)
return items[:n]
User-Based 和 Item-Based 的对比
| * | UserCF | ItemCF |
|---|---|---|
| 性能 | 适用于用户较少的场合,如果用户很多,计算用户相似度矩阵代价很大 | 适用于物品数明显小于用户数的场合,如果物品很多(网页),计算物品相似度矩阵代价很大 |
| 领域 | 时效性较强,用户个性化兴趣不太明显的领域 | 长尾物品丰富,用户个性化需求强烈的领域 |
| 实时性 | 用户有新行为,不一定造成推荐结果的立即变化 | 用户有新行为,一定会导致推荐结果的实时变化 |
| 冷启动 | 在新用户对很少的物品产生行为后,不能立即对他进行个性化推荐,因为用户相似度表是每隔一段时间离线计算的。新物品上线后一段时间,一旦有用户对物品产生行为,就可以将新物品推荐给和对它产生行为的用户兴趣相似的其他用户。 | 新用户只要对一个物品产生行为,就可以给他推荐和该物品相关的其他物品。没有办法在不离线更新物品相似度表的情况下将新物品推荐给用户 |
| 推荐理由 | 很难提供令用户信服的推荐解释 | 利用用户的历史行为给用户做推荐解释,可以令用户比较信服 |
3.4 Memory-Based 算法的扩展
3.4.2 逆用户频率
两个用户同时购买了一些普遍需要的 item,这可能并不能说明这两个用户是相似的。而两个用户同时购买了一些小众的物品,这就很能说明他们是相似的。逆用户频率就是考虑到了这一点,因此在对 item 的评分值上乘以一个因子:
\[f_{j}=\log \left(n / n_{j}\right)\]n 是所有用户数,而 n_j 是给 item j 评分过的用户数。
3.4.3 权重调整
为了排除干扰,对于权重小的(相似度低的)user 或 item 我们希望过滤掉,排除噪音。但是有时候又不能直接设置一个阈值来把小于某个阈值的相似度直接置为 0,那么可以采用下面的式子对原始权重进行变化。下面的式子对于小的权重会急剧缩小,对于大的权重会放大,对于中等的权重会大致保持原来的样子,如 0.1^2.5 = 0.0032, 0.9^2.5 = 0.7684 。这里 p 通常 > 1, 一个典型值为 2.5。
\[w_{i, j}^{\prime}=w_{i, j} \cdot\left|w_{i, j}\right|^{\rho-1}\]式子中增加了一个绝对值,以保证符号不变。
6. 评价指标
MAE
在预测评分的场景下,推荐算法给根据训练集来预测测试集中的评分,并与测试集真实评分比较。这种场景可以采用 Mean Absolute Error (MAE)。
\[M A E=\frac{\sum_{\{i, j\}}\left|p_{i, j}-r_{i, j}\right|}{n}\]$n$ 是预测的所有评分的数量,$p_{i,j}$ 是预测的 user i 对 item j 的评分,$r_{i,j}$ 是真实评分。
RMSE
Root Mean Squared Error (RMSE) 式子如下,符合意义和前面 MAE 中相同。
\[R M S E=\sqrt{\frac{1}{n} \sum_{\{i, j\}}\left(p_{i, j}-r_{i, j}\right)^{2}}\]RMSE 取了误差的平方,这会放大较大的误差。
def RMSE(pred, true):
square_sum = sum((p - r)**2 for p, r in zip(pred, true))
return math.sqrt(square_sum / len(pred))
def MAE(pred, true):
absolut_sum = sum(abs(p - r) for p, r in zip(pred, true))
return absolut_sum / len(pred)
RMSE([3.7, 2], [0.7, 1.2]) # 2.2
MAE([3.7, 2], [0.7, 1.2]) # 1.9
有时候平均指标,如 RMSE 虽然很小,但是在实际应用中,不见得越小越好。比如用户可能更喜欢推荐给他一些不那么熟悉的物品。而不是那些在指标上表现很好,但是用户因为见得太多,已经有些厌倦的物品。